In this article, we will learn how to choose the solver for our analyses, a choice to be made depending on the model to be calculated and for which types of analysis.
Not all solvers are the same. NextFEM Designer supports 3 different solvers:
- The default solver, a custom version of OOFEM,
- OpenSees,
- CalculiX.
Not all solvers are suitable for all models, because their capabilities are different even though they all perform so-called structural analysis. The first distinction must be made on the type of model and which elements it is composed of. A mechanical engineer will in fact be interested in different results from those sought by a civil engineer, because the object analysed changes even with the same type of analysis (e.g. non-linear static analysis):
- for the former will be a mechanical part, for which it will be important to analyse the stresses in the structure, model parts in contact and use a non-linear material model,
- in the design of constructions, one wants to evaluate the stress in each element of the structure at a different scale, considering macroscopic effects such as earthquake, and possibly a concentrated plasticity already preconfigured in certain positions of the model (e.g. at beam ends, with plastic hinges).
Well, the choice of solver can influence the type of results obtained and the possibilities of analysis:
- The default solver allows all analyses that can be set up in NextFEM Designer and is optimised for all types of results to be provided (stresses, strains, forces and moments per unit length) in all types of elements (springs, rods, beams, shells, solids).
-
The
OpenSees solver, which can be downloaded from its official website, makes it
easy to perform nonlinear analyses with improved convergence. This is why
NextFEM Designer also supports OpenSees all its nonlinear elements, springs and
hinges.
OpenSees is developed in an academic research environment, and does not always
include the stress recovery procedures required by the user. NextFEM Designer
compensates for this by implementing, for example, the restitution of stresses
at nodes instead of Gauss points for shell elements, or the reconstruction of
stress diagrams for beam elements.
Finally, NextFEM Designer was the first to support response spectrum (RS)
analyses in OpenSees via an external library. Although now supported directly
in OpenSees, Designer conducts RS analyses with its own library that was
developed and validated in-house.
- The CalculiX solver, which can be downloaded in its Windows version from the website of its main developer, is a solver that focuses on the mechanical part, e.g. expanding beams with rectangular and circular cross-sections into solids and then proceeding with the calculation. PDelta analyses for 2-node beam elements, RS analyses and analyses with non-linear spring or hinge elements are not supported in this solver. It is therefore preferable for analyses with solids, both first-order (tetra, wedge, hexa) and second-order (tetra10, wedge15, hexa20), which NextFEM Designer supports. In CalculiX, all loads are reported at nodal loads.
The solver settings are summarised in the mask Options / Solver tab.
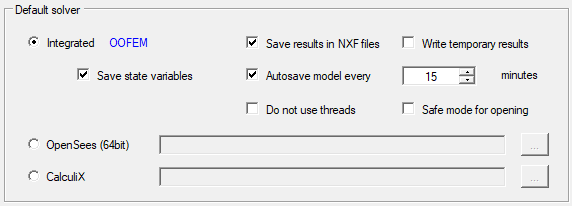
It is then possible to analyse a model with all supported solvers in an equivalent manner. For calculation validation purposes, it is possible, for example, to analyse a structure with the integrated solver and then with OpenSees to compare the results, especially with regard to static or dynamic nonlinear analyses.
For the default solver, you can also choose the solver type of the system of equations in the Solver box.
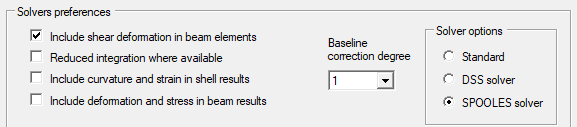
- Standard is a solver that is not optimised for speed, but is able to signal the presence of any lability and identify the node that causes it;
- DSS is a fast solver that saves RAM during calculation; it is therefore suitable for very large models;
- SPOOLES is also a fast solver, which maximises speed with respect to memory occupation. It is therefore preferable once there is no lability to be found in the model.
In the same box as the solver options, we find an option relating to the 'Degree of baseline correction', which affects only linear dynamic analyses and not those with one or more baseline accelerograms as input. The number specifies the degree of the polynomial used to return the displacement history derived from the acceleration history to a final null displacement; in other words, it serves to cancel the absolute residual ground displacement typical of seismic recordings.